Figure 18b. DC Equivalent of circuit 18a.
Figure 18a shows an AC amplifier that works with a single power supply. In this amplifier the load RL, and the signal source are connected directly to the earth and not with the VBias voltage.
Therefore, the voltage applied to the input (VP) of the operational amplifier is equal to the voltage bias (VBias). The voltage in the reverse input VN, is equal to:
VN = VD + VP
And since in an ideal operational amplifier, VD = 0, we have:
VN = VP
Therefore, both inputs of the operational amplifier having the same voltage (equal to VBias). The input capacitor (Cin) blocks the flow of direct current through the resistor R1.
Therefore, on the direct current circuit of Figure 18 is equivalent to the circuit shown in Figure 18b, which is a voltage follower with voltage gain equal to the unit (AV = 1). Therefore, the constant voltage applied to the input is equal to VBias and the voltage at the output is equal to:
V0 = AV x VBias = 1xVBias
Therefore, the two inputs and the output of the operational amplifier have the same voltage (VBias). If VBias = VCC / 2, then the inputs and the output are located between +Vcc and ground (0 volts), and therefore the amplifier allows the positive and the negative change at the output signal. The output voltage of the amplifier can be determined as follows: The current I1 flowing through the resistor R1 and the capacitor CIN is equal to the current I2 flowing through resistor R, so we say:
I1 = I2
The current flowing through R1 is equal to the voltage difference between the combination of the range R1 and CIN, ie we have:
Where VA = VIN,
VB = VP = VD + VBias = VBias (because VD = 0)
Also:
So:
The current I2 is equal to
Since I1 = I2 we have:
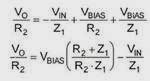
From the above equation we get:
By multiplying both sides with R2 we have:
Figure. 19
Note that the expression in the first part in brackets of equation 2, represents the voltage gain of an amplifier to correct AC wiring, and the second part in brackets represents the second voltage gain of an amplifier in reverse AC wiring. Substituting the value of Z1 in the above equation we get:
At rest, VIN = 0V, and since the impedance of a capacitor (capacitance Xc = 1/2pfC) to direct current (f = 0Hz) is essentially infinite, the output voltage is:

Because R2 / infinity = 0
We have:
V0 = VBias(0 + 1) = VBias
Vo = VBias
From the above equation we see that the output voltage is equal to the polarization voltage (VBias). Therefore, the voltage at both inputs and the voltage output of the operational amplifier are equal. Due to the presence of the input capacitor, the voltage gain of the amplifier AC now depends on the frequency of the signal applied to the input of the amplifier. The capacitor CIN input and resistor R1 form a high pass RC filter. The values R1 and CIN determine the low cut-off frequency of the amplifier. The frequency at which the voltage gain is decreased by -3dB, is the low cut-off frequency, and can be determined using the following equation:
For example, if CIN = 1pF and R1 = 10Kohm, then the low frequency cutoff is 15.9Hz. Signals having lower frequency than the cutoff frequency, are reduced by 20 decibels (20 decibels per decade) for each tenfold reduction in frequency (one decade corresponds to a ten-fold increase or decrease in frequency). If a capacitor is connected in series with the output, the capacitor will prevent the DC current and will only allow the AC signal to pass, and thus the bias voltage to the load by changing the voltage VBias of the earth (0 volts). The capacitor output together with the load RL forms a low pass RC filter which causes attenuation at low frequencies. Note that although the circuit shown in Figure 16 uses the smallest number of components, may be unsuitable in certain applications where the signal source, the load, and the proper input of the operational amplifier, it must be connected to a bias voltage in such cases should use the circuit shown in Figure 18. Notice that the voltage gain in the circuit shown in Figure 18 depends on agreements frequencies, due to the presence of the input capacitor. You may think that the circuit shown in Figure 18 will work correctly if removing the input capacitor CIN (Fig. 19), but, this capacitor must remain otherwise the circuit will not work correctly. The output voltage of the amplifier in Figure 19 is given by the following equation:
The above equation can be proved very simply by using the principle of ultra-rustling, as follows: First we set VBias = 0, the amplifier is now essentially an inverse amplifier and the output voltage is given by the following equation:
VO(-) = VIN x (-R2/R1)
V0(+) = VBias (1 + R2/R1)
V0 = V0(-) + V0(+), or Observe that The above equation is the same as Equation 2 if you replace Z1 with R1.
Figure 20. AC amplifier.
In the absence of an input signal, the dc voltage at the output will try to become equal with
For example, if R1 = R2 = 10Kohm, Vcc = 10V, and VBias = 5V, then:
V0 = (1 +2) VBias = (3)x(5V) = 15V
However, this is not possible because the maximum positive output voltage can have with this amp is less than +10 V.
Therefore, the output voltage is always less than the positive voltage of the power supply. Therefore, when an input signal applied alternating current, the output remains saturated during the negative half-period of the input signal. The output will also remain saturated just below the positive trend of +10 V of power supply, for the positive input signals. The circuit shown in Figure 20 is a correct AC amplifier that operates with a single power supply. The voltage between the reverse and correct input is substantially equal to zero volts. After VN = VD + VP and VD = 0, the input terminal of the reverse is also VBias = Vcc/2, relative to the earth. Therefore, both inputs of the operational amplifier is at the same voltage (VBias). The output voltage can be determined as follows:
The current I1 flowing through Z1 is equal to the current I2 flowing through resistor R2. The voltage across Z1 is equal to VB-VA, where VB = VBias and VA = 0.
So we have:
The voltage across R2 is equal to:
Vo = VB: therefore
Since I1 = I2, we have:
Again rearranging the above equation we take:
By multiplying both sides with R2 we get:
The impedance Z1 is given by the equation:
At DC (f = 0Hz), the resistance of the capacitor Cin is infinite:
Consequently in DC we get:
and so VO = VBias.
We will now examine the various circuits to generate the dc voltage bias, which is sometimes called virtual ground. Before you choose a circuit output dc voltage bias must specify load regulation, power supply rejection, power dissipation and the output impedance of the circuit bias. The final decision on what bias circuit will be used in an application depends on the cost and the space we have available to us. The simple voltage divider shown in Figure 21, can be used to produce the constant bias voltage (VBias). This circuit has low load regulation. I.e. as the load current increases, the output voltage of this circuit (bias voltage) is reduced. An explanation of the load regulation and line regulation given below.
Figure 21
Figure 22
Figure 22(a). Equivalent circuit of an ideal power supply, (b) Equivalent circuit of an actual power supply.
An ideal power supply provides an output voltage that remains constant regardless of the load current, and is also independent of temperature variations, and also from any changes in the supply voltage of the alternating current network. Figure 22A shows the equivalent circuit of an ideal power supply. In the case of a practical power supply, the output voltage decreases as the load current increases. This is why a real power has an equivalent internal resistance, because of the various components of which consists of the power supply circuit. The equivalent circuit of an actual power supply shown in Figure 22b, where VNL is the output voltage with an open circuit (ie the output voltage when there is no load at the output terminals of the power supply), and R1 is the total internal resistance of the power supply. When a load is connected to the output of the power supply, the output voltage, ie the voltage across the load (VL = IL x RL) is less than the output voltage (VNL) with open circuit. This is because the resistors RL, and RI, form a voltage divider and the voltage across the load is given by:
When the load current increases, the voltage drop across the internal resistance RI also increases, and therefore, the output voltage decreases. The reduction of the output voltage as the load current increases, is a disadvantage. The output voltage of a typical power supply compared to the load current is shown in Figure 23. An ideal power supply has an output voltage that is constant regardless of the load that connects to the output terminals. Obviously, if the internal resistance RI is zero or very small compared to the RL, then output voltage VO is constant and equal to the VNL. The change of the DC output voltage of the power supply relative to the continuous load current is called, simply load regulation or regulation.
The regulation is defined as follows:
The load regulation can be expressed as a percentage:
An ideal power supply would have 0 load regulation, since an ideal power supply is:
RI = 0, and therefore VL = VNL.
Example. The open circuit voltage (i.e., when RL = infinity) of a power supply is VNL = 20V, and when a load is connected to terminals of the power supply, the output voltage drops to 15V. The load regulation of the power supply is given by:
Figure. 23
Ie the regulation of the power supply is 25%.

























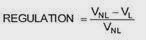




0 comments:
Post a Comment